數學家用全新數列解開代數最古老難題
澳洲新南威爾斯大學(UNSW)的數學家 Norman Wildberger 教授,近日發表突破性研究,提出一種全新方法來解決代數中最古老也最難的問題之一:高次多項式方程的通解。該成果已刊登於《The American Mathematical Monthly》。
從二次方程式到四次方程式,數學家早在 16 世紀就能利用「根式」(radicals)求解。但 1832 年,法國數學家加羅瓦證明五次以上的多項式無法以一般方式解出。此後,雖有許多數值近似法被廣泛應用,但一直沒有純代數意義上的通解。
Wildberger 教授的創新之處,在於拒絕使用傳統根式和無理數。他主張無理數建立在無限這個「不精確」概念上,導致邏輯混亂。他提出的解法不依賴無窮小數,而是使用可截斷的「冪級數」(power series)和全新的組合數列,稱為「Geode」。
不依賴無窮小數,而使用可截斷的「冪級數」
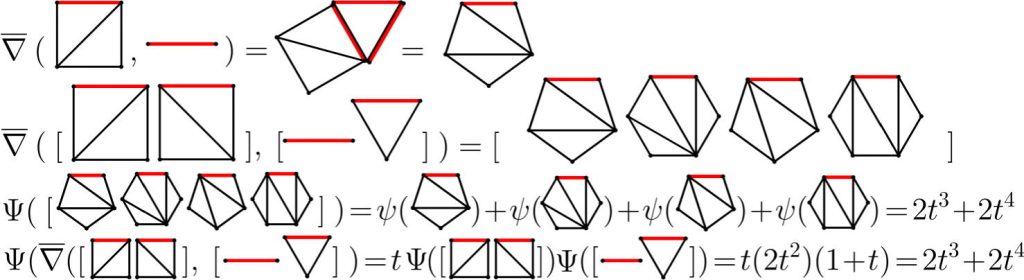
圖形意義:圖中是各種多邊形被不相交線段分割成三角形(稱為 triangulation)的方法,每種不同的分割對應一種「組合結構」,這些結構可以被編碼為數列,進而應用於解多項式。
紅色邊線:紅色邊線標示的是一種特定的「操作邊」或被觀察的關鍵部分,常用來定義遞迴式或特定條件。
符號說明:
∇:代表某種「分割操作」,將複雜圖形拆解為較簡單單元。
Ψ:是一個對應的函數映射,用來把圖形組合轉換成代數形式的多項式。例如:Ψ(某組圖形) = 2t³ + 2t⁴,代表這組結構的計數權重。
ψ:是 Ψ 的基本單位計算。
主要數學重點:這些圖形的分割數量與方式,對應到特定係數的多項式。這樣的多項式再被用來解多項式方程本身,因此從「圖形分割」可直接導出方程的近似解。
圖片說明的是:把多邊形劃分成三角形的所有方法,可以用來構造一種新的數列系統,而這些數列就可以用來解代數裡的高次方程。這就是 Wildberger 所提出「Geode 數列」的核心概念之一,把幾何圖形結構轉化為代數資訊。(圖/《The American Mathematical Monthly》)
這些數列靈感來自著名的「Catalan 數」,後者描述將多邊形分割成三角形的方式,廣泛應用於資料結構、演算法與 RNA 摺疊路徑等領域。Wildberger 將其從一維推廣至多維,捕捉多邊形內部不相交分割的所有可能性,進而建立出可套用至任意次多項式的解法架構。
研究還展示了使用 Geode 處理古典三次方程(如 Wallis 方程)的優異效果,驗證此方法具實用潛力。Wildberger 表示,這項發現不僅為理論數學帶來突破,也可能推動演算法革新,提升解方程式的電腦運算效率。
他認為 Geode 數列背後蘊藏豐富數學結構,有望開啟全新研究領域。「這只是個開始,組合數學家未來幾年恐怕都忙不完。」
更多科學與科技新聞都可以直接上 明日科學網
首圖來源:UNSW Sydney (CC BY 4.0)
圖片來源:The American Mathematical Monthly (CC BY 4.0)
參考論文:
1、A Hyper-Catalan Series Solution to Polynomial Equations, and the Geode