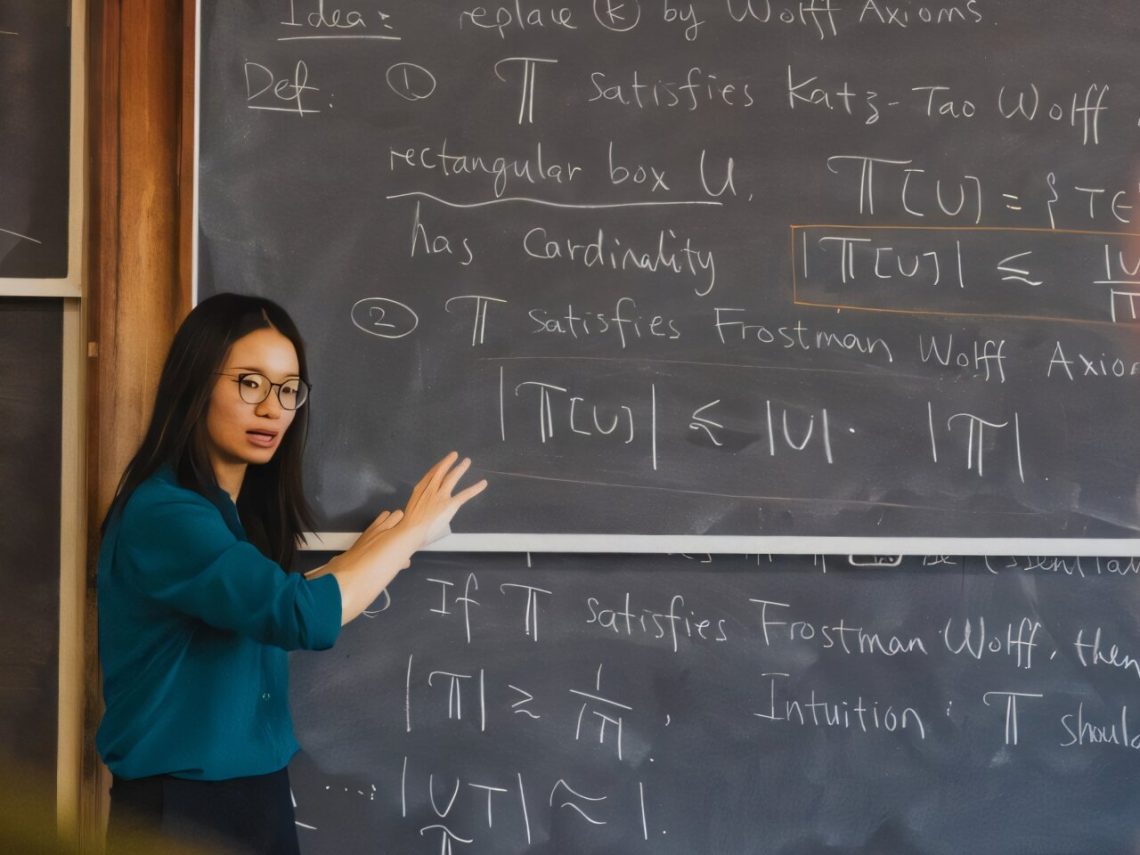
數學家破解卡谷谷(Kakeya)猜想三維版本,改寫幾何學發展
數學家來自紐約大學與英屬哥倫比亞大學的團隊成功解決了一個長達數十年的幾何難題——卡谷谷猜想(Kakeya conjecture)在三維空間的版本,這項研究已發表於 arXiv 預印本平台。
卡谷谷猜想源自 1917 年日本數學家卡谷谷宗一(Sōichi Kakeya)提出的問題:在平面上,讓一根針旋轉 180 度所需的最小區域是什麼?這類區域被稱為卡谷谷針集(Kakeya needle sets)。過去的研究顯示,這些集合的面積可以趨近於零,但在三維空間內,對應的「卡谷谷集」是否也能極小化,仍未被證明。
此次研究由紐約大學克朗數學研究所(Courant Institute)副教授王泓(暫譯,英文名為Hong Wang)與英屬哥倫比亞大學數學系副教授喬舒亞·扎爾(Joshua Zahl)合作完成。他們證明了,雖然卡谷谷集的體積可以為零,但它們仍必須具有三維結構,這解決了長期懸而未決的幾何測度理論難題。
推動訊號處理與數據分析發展
此突破亦獲得數學界高度評價。曾獲 2006 年菲爾茲獎(Fields Medal)的加州大學洛杉磯分校(UCLA)數學教授陶哲軒(Terence Tao)稱這是幾何測度理論的一大進展。紐約大學數學系主任 Eyal Lubetzky 甚至表示,這項研究堪稱 21 世紀最重要的數學成就之一。
專家指出,這項證明運用了尺度歸納法(induction on scales),並在研究管狀結構交錯(tube intersections)方面提出了比卡谷谷猜想更普遍、更易於處理的理論。研究成果不僅影響幾何學,還將在諧波分析、數論、計算機科學與密碼學等領域帶來潛在應用,例如解釋波動包(wave packets)在空間中的交互作用,進一步推動訊號處理與數據分析的發展。
更多科學與科技新聞都可以直接上 明日科學網
首圖來源:David Song/NYU (CC BY 4.0)
參考論文:
Volume estimates for unions of convex sets, and the Kakeya set conjecture in three dimensionsarXiv